JeongMin-힙(heap)

힙(Heap)

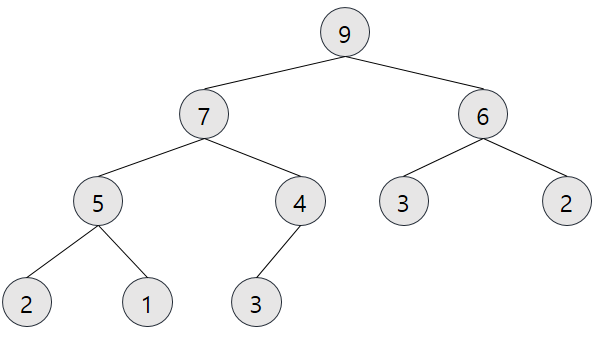
heap

힙은 힙의 특성(최소 힙에서는 부모가 항상 자식보다 작거나 같다)을 만족하는 거의 완전한 트리인 특수한 트리 기반의 자료구조

완전 이진 트리 기반의 최댓값과 최솟값을 빠르게 찾아내기 위한 자료구조

히프 트리에서는 중복된 값 허용
반정렬상태(큰 값이 상위에 있고 작은 값은 하위에 있음)
부모의 인덱스 찾는 방법
- 부모 인덱스 = (자식의 인덱스) / 2
자식의 인덱스 찾는 방법
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1

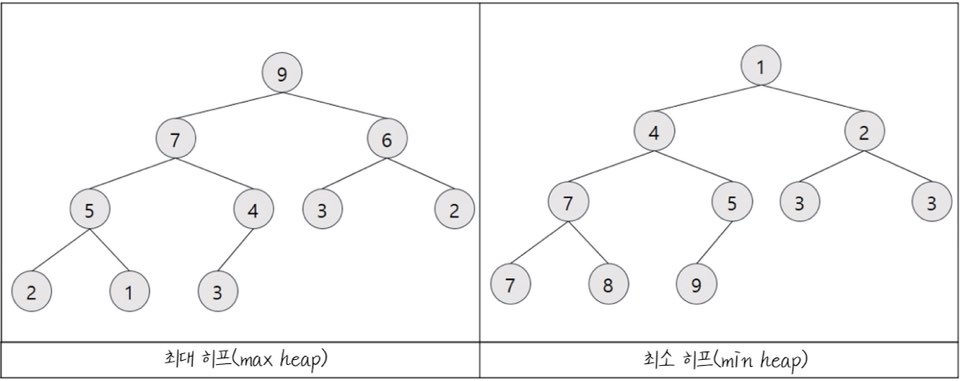
힙 종류

max_min_heap

최대 히프(max heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
  
  key(부모 노드) ≥ key(자식 노드)
최소 히프(min heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
  
  key(부모 노드) ≤ key(자식 노드)

파이썬 heapq

heapq모듈은 이진 트리 기반의 최소 힙(min heap)을 제공한다. 최소 힙은 가장 작은 값이 인덱스 0에 위치하며, 모든 k에 대해 heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2]

힙 생성

import heapq
heap =[]

요소 추가 `heapq.heappush(heap, item)`

heap은 원소를 추가할 대상 리스트이며, item는 추가할 원소를 의미한다.

heapq.heappush(heap, 1)
heapq.heappush(heap, 4)
heapq.heappush(heap, 7)
heapq.heappush(heap, 3)
# [1, 3, 7, 4]

가장 작은 값이 인덱스 0에 위치하며, 인덱스 1(=k)에 위치한 3은 인덱스 3(=2*k+1)에 위치한 4보다 작으므로 힙의 공식을 만족한다.

요소 삭제`heapq.heappop(heap)`

원소를 삭제할 대상을 넘기면, 가장 작은 원소를 삭제 후 그 값을 리턴한다.

heap.heappop(heap)
# 1
# [3, 4, 7]

삭제하지 않고 최솟값 얻기`heap[0]`

리스트와 같이 인덱스로 접근하면 된다. 하지만, 인덱스 1에는 두번째로 작은 원소, 인덱스 2에는 세번째로 작은 원소가 있는 것이 아니다. 따라서 n번째로 작은 원소를 얻고 싶으면 n-1번 pop한 후 인덱스0을 추출해야한다.

print(heap[0])
# 3

아래의 사진을 보면 pop하는 순간 트리가 재정렬되면서 인덱스와 값이 바뀐 것을 파악할 수 있다.

리스트를 힙으로 변환`heapq.heapify(list)`

heap_list = [4, 6, 1, 8, 2, 3, 9]
heapq.heapify(heap_list)
print(heap_list)
# [1, 2, 3, 8, 6, 4, 9]

최대 & 최소값 찾기`heapq.nlargest(n, list, key=None)`

import heapq
list = [3, 2, 1, 5, 6, 4]
print(heapq.nlargest(2, list))
# [6, 5]
print(heapq.nsmallest(3, list))
# [1, 2, 3]

# 키를 사용한 경우
data = [
    {'name':'AAA', 'math':80, 'eng':60},
    {'name':'BBB', 'math':90, 'eng':85},
    {'name':'CCC', 'math':20, 'eng':65},
    {'name':'DDD', 'math':45, 'eng':100},
    {'name':'EEE', 'math':70, 'eng':25},
]
eng_king = heapq.nlargest(2, data, key=lambda x: x['eng'])
print(eng_king)
# [{'name': 'DDD', 'math': 45, 'eng': 100}, {'name': 'BBB', 'math': 90, 'eng': 85}]

힙의 시간 복잡도

함수	시간복잡도
heappush	O(logN)
heappop	O(logN)
heapify	O(N)

최대 힙(max heap)

import heapq

nums = [4, 1, 7, 3, 8, 5]
heap = []

for num in nums:
    heapq.heappush(heap, (-num, num)) # (우선순위, 값)
    
while heap:
    print(heapq.heappop(heap)[1])
# 8
# 7
# 5
# 4
# 3
# 1

이진 힙 구현

class BinaryHeap(object):
    def __init__(self):
        self.items = [None]
    
    def __len__(self):
        return len(self.items) - 1
    
    # 힙 삽입 -> 시간복잡도 O(log n)
    # 1. 요소를 가장 하위 레벨의 최대한 왼쪽으로 삽입(배열에서는 가장 마지막을 의미)
    # 2. 부모 값과 비교해 값이 더 작은 경우 위치를 변경
    # 3. 계속해서 부모 값과 비교해 위치를 변경(가장 작은 값일 경우 루트까지 올라감)
    def _percolate_up(self):
        i = len(self)
        parent = i // 2
        while parent > 0:
            if self.items[i] < self.items[parents]:
                self.items[parent], self.items[i] = self.items[i], self.items[parent]
                
            i = parent
            parent = i // 2
    
    def insert(self, k):
        self.items.append(k)
        self._percolate_up()
                
    # 힙 추출 -> 시간복잡도 O(log n)
    # 1. 루트 추출
    # 2. 가장 마지막 요소가 루트로 올라감
    # 3. 자식 노드와 값을 비교해 자식 보다 크면 다운힙 연산 수행
    def _percolate_down(self, idx):
        left = idx * 2
        right = idx * 2 + 1
        smallest = idx
        
        if left <= len(self) and self.items[left] < self.items[smallest]:
            smallest = left
        
        if right <= len(self) and self.items[right] < self.items[smallest]:
            smallest = right
        
        if smallest != idx:
            self.items[idx], self.items[smallest] = self.items[smallest], self.items[idx]
            self._percolate_down(smallest)
            
    def extract(self):
        extracted = self.items[1]
        self.items[1] = self.items[len(self)]
        self.items.pop()
        self._percolate_down(1)
        return extracted

이진 힙 vs 이진 탐색 트리

차이점

힙은 상/하 관계를 보장하며, 특히 최소 힙에서는 부모가 항상 자식보다 작다.
이진 탐색 트리(BST)는 좌/우 관계를 보장하며, 부모는 왼쪽의 자식보다는 크며 오른쪽 자식보다는 작거나 같다.
BST는 탐색과 삽입 모든 O(log n)에 가능하며, 모든 값이 정렬되어야 할 때 사용
가장 큰 값을 추출하거나(최대 힙) 가장 작은 값을 추출하려면(최소 힙) 이진 힙을 사용해야 함 -> O(1)에 가능

힙(heap)