해시 테이블(hash table)

해시 테이블(hash table)

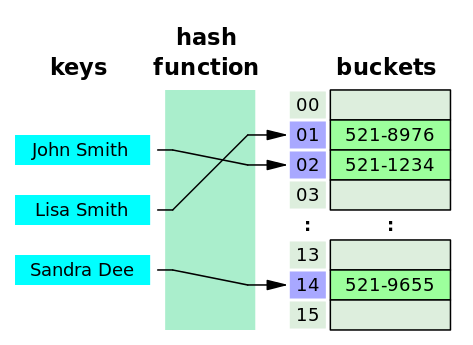
키(key)와 값(value) 쌍으로 이루어진 자료구조

장점

• 데이터 저장/검색의 속도가 빠름
• 해쉬는 키에 대한 데이터가 있는지(중복) 확인이 쉬움

단점

• 저장공간이 많이 필요
• 여러 키에 해당하는 주소가 동일할 경우 충동을 해결하기 위한 별도의 자료구조가 필요

용어

• 해쉬(hash) : 임의 값을 고정 길이로 변환하는 것을 의미
• 해쉬 함수(hash function) : 특정 연산을 이용해 키 값을 받아 value를 가진 공간의 주소로 바꿔주는 함수를 의미
• 해쉬 테이블(hash table) : 해쉬 구조를 사용하는 데이터 구조
• 해쉬 값(해쉬 주소, hash value/address) : key값을 해쉬 함수에 넣어서 얻은 주소값을 의미, 이 값을 통해 슬롯을 찾아감
• 슬롯(slot/bucket) : 한 개의 데이터를 저장할 수 있는 공간

해시 함수

나눗셈 방식(Modulo-Division Method)

나머지 연산자를 사용하여 탐색 키를 해시 테이블의 크기로 나눈 나머지를 해시 주소로 사용하는 방법

• m으로 나눈 나머지 값의 범위는 0~(m-1)이 되으모 해시 테이블의 인덱스로 사용 가능
• 해시 주소는 충돌이 발생하지 않고 고르게 분포하도록 생성되어야 함
• 따라서, 해시 테이블의 크기인 m은 일반적으로 소수를 사용

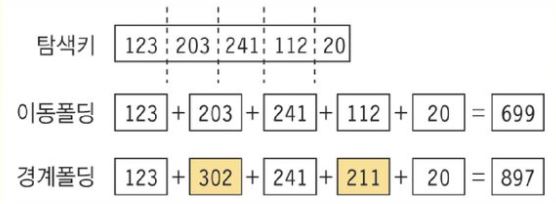
폴딩 함수

탐색 키를 여러 부분으로 나누어 모두 더한 값을 해시 주소로 사용하는 방법

• 탐색키를 나누고 더하는 방법에는 이동 폴딩(shift folding)과 경계 폴딩(boundary folding)이 대표적
• 이동 폴딩(shift folding) : 탐색 키를 여러 부분으로 나눈 값들을 더하여 해시 주소로 사용
• 경계 폴딩(boundary folding) : 탐색 키의 이웃한 부분을 거꾸로 더하여 해시 주소로 사용

충돌

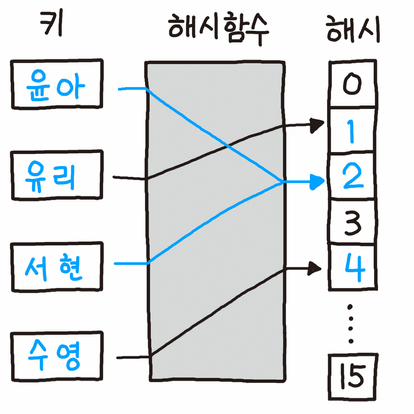
서로 다른 탐색 키를 갖는 항목들이 같은 해시 주소를 가지는 현상을 의미

개별 체이닝(Separate Chaining)

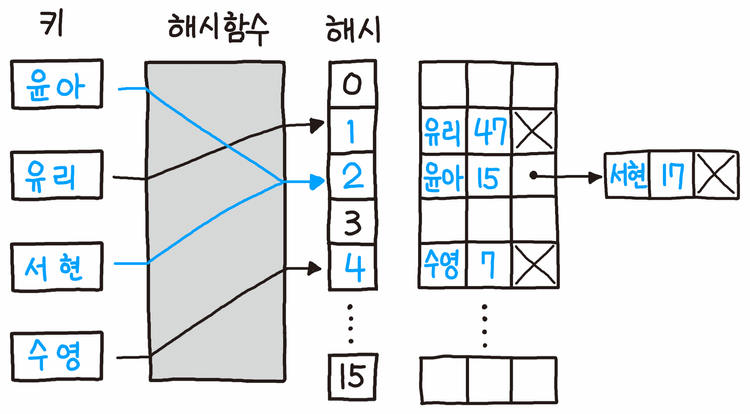
개별 체이닝은 충돌 발생 시 연결 리스트로 연결하는 방식이다.

• 무한정 저장 가능

• 탐색 키들의 중복을 허용하면 연결 리스트의 처음에다가 삽입한다.
• 탐색 키들의 중복을 허용하지 않으면 연결리스트의 뒤에 삽입한다.

원리

1. 키의 해시 값을 계산한다.
2. 해시 값을 이용해 배열의 인덱스를 구한다.
3. 같은 인덱스가 있다면 연결 리스트로 연결한다.

시간 복잡도

대부분의 탐색은 O(1)이지만 최악의 경우, O(n)이 된다.

오픈 어드레싱(Open Addressing)

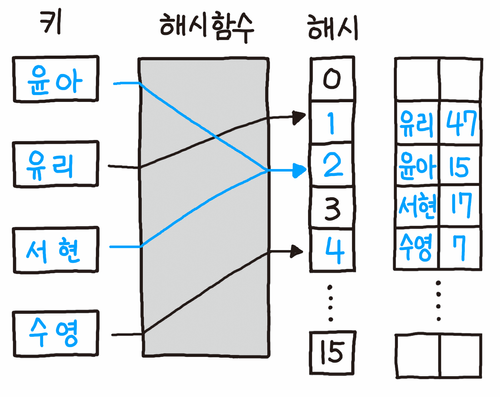
오픈 어드레싱 방식은 충동 발생 시 해시 테이블에서 비어있는 공간을 찾는 방식이다.

• 조사(probing) : 비어 있는 공간을 찾는 것
• 전체 슬롯의 개수 이상은 저장 불가능
• 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장이 없음

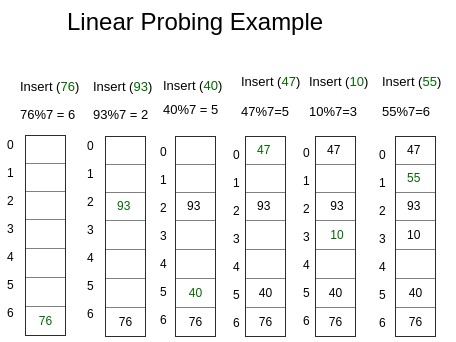
선형 탐사(Linear Probing)

충돌이 발생한 경우 해당 위치(k)부터 순차적(k+1, k+2…)으로 탐사를 하나씩 진행하다가 비어있는 공간을 발견하면 삽입하는 방식이다.

• 장점 : 구현이 간단하며 성능이 좋음

• 단점 : 해시 테이블에 저장되는 데이터들이 고르게 분포되지 않고 뭉치는 경향이 있음

• 버킷 사이즈보다 큰 경우에는 삽입이 불가

• 따라서 일정 이상 채워지면 (로드 팩터의 비율을 넘으면) 그로스 팩터의 비율에 따라 더 큰 크기의 다른 버킷을 생성한 후 복사하는 리해싱(Rehasing) 작업 발생