그래프(graph)

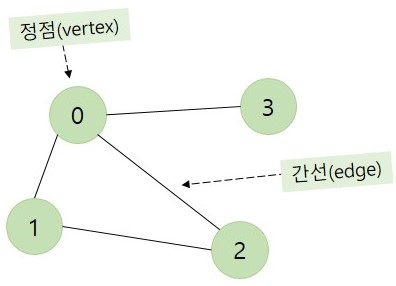
graph

연결되어 있는 객체 간의 관계를 표현할 수 있는 자료 구조

그래프는 정점과 간선의 집합으로 구성되며, 정점은 노드라고도 불리고 간선은 링크라고 불린다.


그래프 표현

인접 행렬(Adjacenecy Marerix)

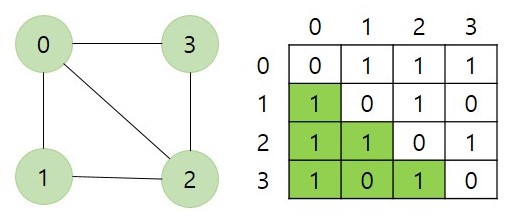
adjacency_matrix

인접 행렬은 그래프를 2차원 배열로 표현한 것

장점

  • 두 정점을 연결하는 간선의 존재 여부를 O(1) 시간 안에 알 수 있다.

단점

  • 모든 정점에 대해 간선 정보를 대입해야 하므로 O(n²)의 시간복잡도가 소요된다.


인접 리스트(Adjacenecy List)

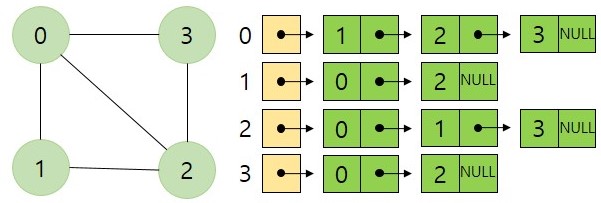
adjacency_list

인접 리스트는 그래프를 표현함에 있어 각각의 정점에 인접한 정점들을 연결 리스트로 표시한 것

장점

  • 정점들의 연결 정보를 탐색할 때 O(n)시간이면 가능 (n: 간선의 갯수)
  • 공간의 낭비가 적음

단점

  • 두 점의 연결 확인 시 인접 행렬에 비해 시간이 오래걸림


그래프 순회

그래프 순회란 그래프 탐색이라고도 불리며 그래프의 각 정점을 방문하는 과정을 말한다.

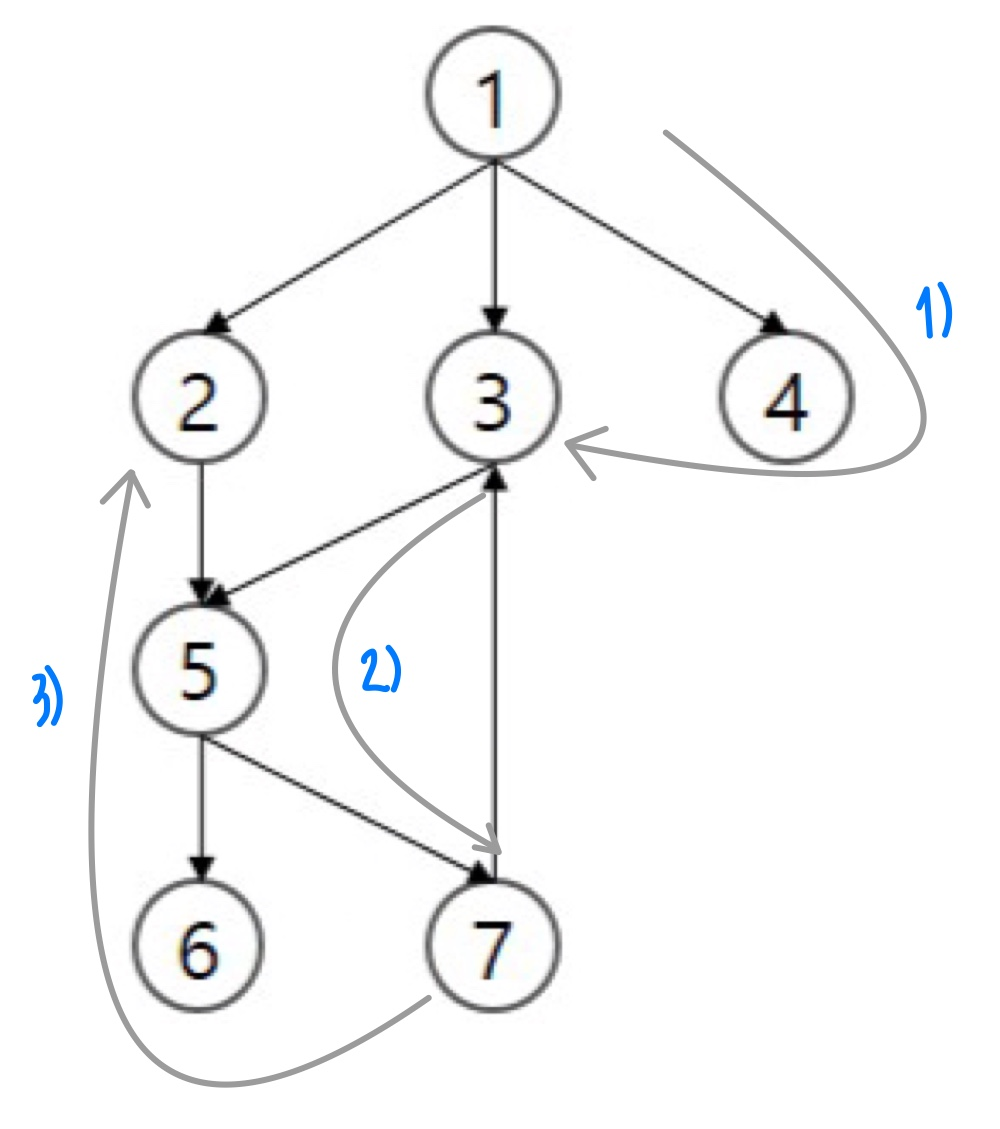
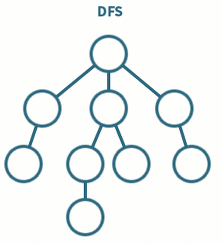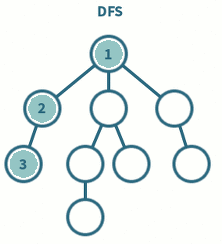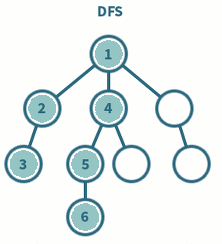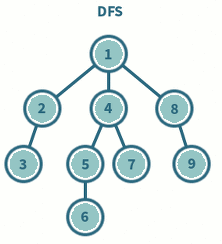
깊이 우선 탐색(Depth First Search : DFS)

DFS

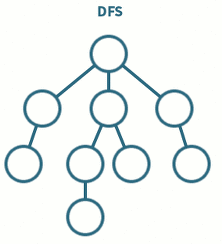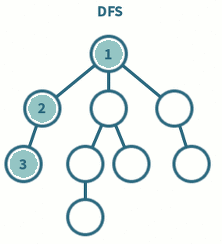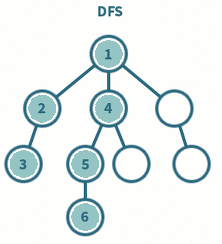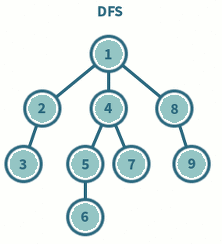
갈 수 있는 만큼 최대한 깊이 가고, 더 이상 갈 곳이 없다면 이전 정점으로 돌아가는 방식

주로 스택이나 재귀, 백트래킹으로 구현


재귀 구조로 구현

graph = {
    1: [2, 3, 4],
    2: [5],
    3: [5],
    4: [],
    5: [6, 7],
    6: [],
    7: [3],
}

def recursive_dfs(v, discovered=[]):
    discovered.append(v)
    for w in graph[v]:
        if not w in discovered:
            discovered = recursive_dfs(w, discovered)
    return discovered

# recursive dfs: [1, 2, 5, 6, 7, 3, 4]

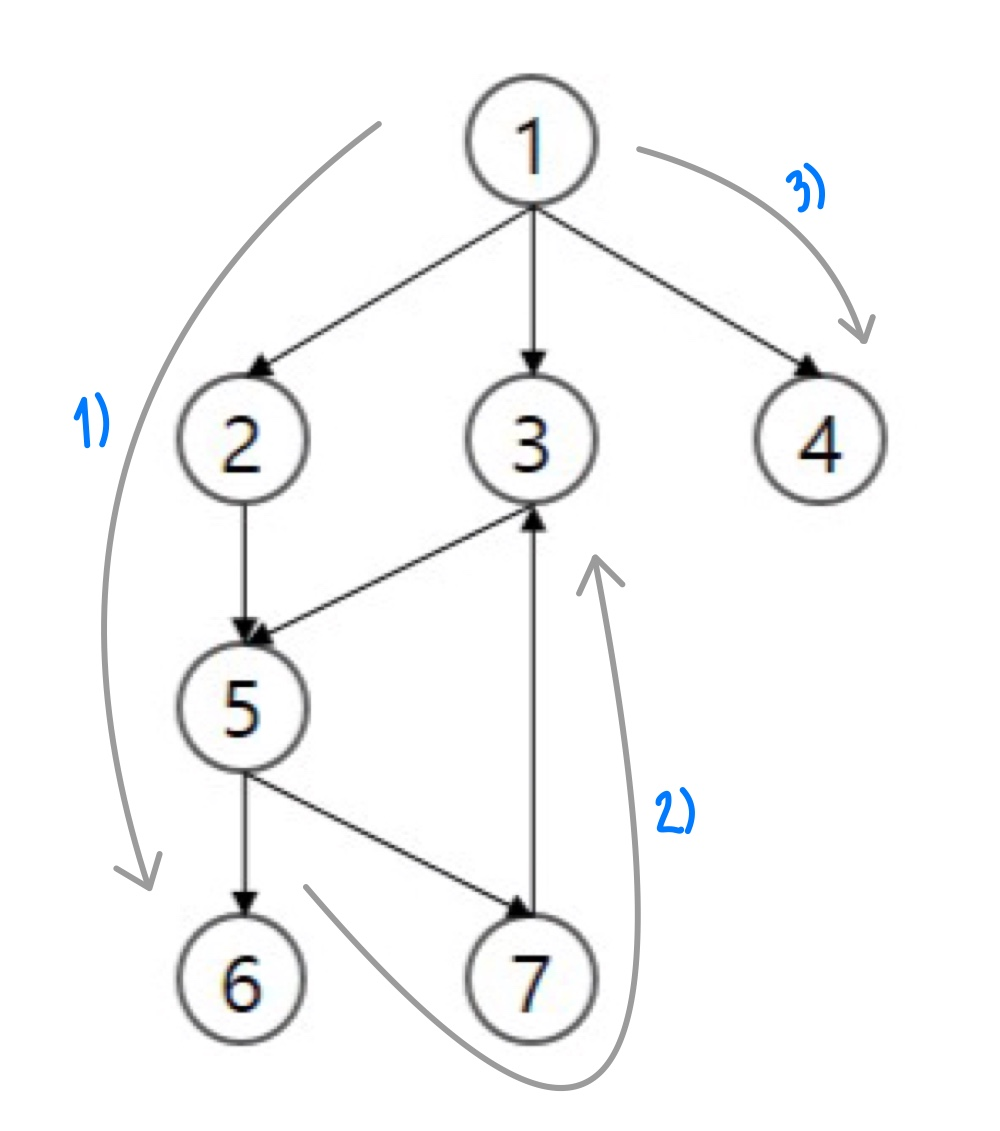
image-20210201174231422


스택을 이용한 반복 구조로 구현

graph = {
    1: [2, 3, 4],
    2: [5],
    3: [5],
    4: [],
    5: [6, 7],
    6: [],
    7: [3],
}

def iterative_dfs(start_v):
    discovered = []
    stack = [start_v]
    while stack:
        v = stack.pop()
        if v not in discovered:
            discovered.append(v)
            for w in graph[v]:
                stack.append(w)
    return discovered

# iterative dfs: [1, 4, 3, 5, 7, 6, 2]

image-20210201175334518


넓이 우선 탐색(Bredth Frist Search : BFS)

BFS

시작 정점을 방문한 후 시작 정점에 인접한 모든 정점을 방문한 후 시작 정좀에 인접한 모든 정점들을 우선 방문하는 방식

주로 큐를 사용해 구현


큐를 이용한 반복 구조로 구현

graph = {
    1: [2, 3, 4],
    2: [5],
    3: [5],
    4: [],
    5: [6, 7],
    6: [],
    7: [3],
}

def iterative_bfs(start_v):
    discovered = [start_v]
    queue = [start_v]
    while queue:
        v = queue.pop(0)
        for w in graph[v]:
            if w not in discovered:
                discovered.append(w)
                queue.append(w)
    return discovered

# iterative bfs: [1, 2, 3, 4, 5, 6, 7]


백트래킹(Backtracking)

해결책에 대한 후보를 구축해 나아가다 가능성이 없다고 판단되는 즉시 후보를 포시(백트랙; Backtrack)해 정답을 찾아가는 범용적인 알고리즘으로 제약 충족 문제에 특히 유용하다.

주로 재귀로 구현


제약 충족 문제

제약 충족 문제란 수많은 제약 조건을 충족하는 상태를 찾아내는 수학 문제를 일컫는다.