트리(Tree)

트리(Tree)

계층형 트리 구조를 시뮬레이션 하는 추상 자료형(ADT)으로, 루트 값과 부모-자식 관계의 서브트리로 구성되며, 서로 연결된 노드의 집합이다.

• 부모-자식 관계
• 트리는 재귀로 정의된 자기 참조 자료구조이다.

트리의 각 명칭

• 트리는 루트(Root)부터 시작하며, 루트는 자식 노드(Child)와 간선(Edge)으로 연결됨
• 리프(Leaf)노드는 자식 노드가 없는 노드를 의미. 단말 노드라 불림
• 차수(Degree)는 자식 노드의 개수를 의미
• 크기(Size)는 자신을 포함한 모든 자식 노드의 개수
• 높이(Height)는 가장 긴 루트 경로의 길이
• 깊이(Depth)는 루트에서부터 현재 노드까지의 거리
• 트리는 그 자식도 트리인 서브트리(Subtree)구성을 가짐
• 레벨(Level)은 0부터 시작
• 내부 정점(Internal vertex)은 차수가 2 이상인 정점을 뜻함
• 포레스트(Forest)는 서로 독립인 트리들의 모임을 의미

그래프 vs 트리

그래프와 트리의 가장 큰 차이점은 트리는 순환 구조를 갖지 않는 그래프이다.

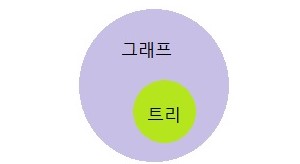
트리도 그래프라 볼 수 있지만, 그래프는 트리라 볼 수 없다.

정리하면,

• 트리는 부모 노드에서 자식 노드를 가리키는 단방향 그래프이다.
• 사이클(순환 구조)를 존재하지 않는다.
• 트리는 하나의 부모 노드를 갖는다.(루트가 하나이다.)

이진 트리(Binary Tree)

부모 노드 밑 자식 노드 개수(=차수)를 최대 2개로 제한하는 트리

이진 트리 유형

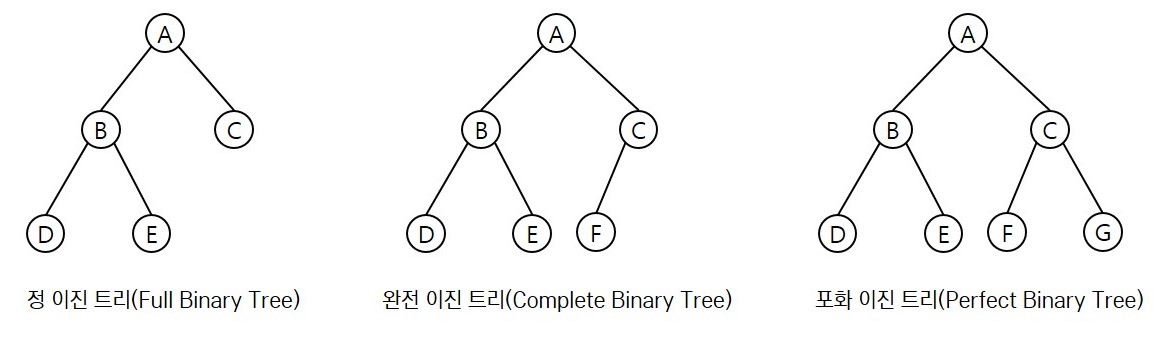
• 정 이진 트리 : 모든 노드가 0개 또는 2개의 자식 노드를 갖는다.
• 완전 이진 트리 : 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있다.
• 포화 이진 트리 : 모든 노드가 2개의 자식 노드를 갖고 있으며, 모든 리프 노드가 동일한 깊이 또는 레벨을 갖는다.

이진 탐색 트리(Binary Search Tree)

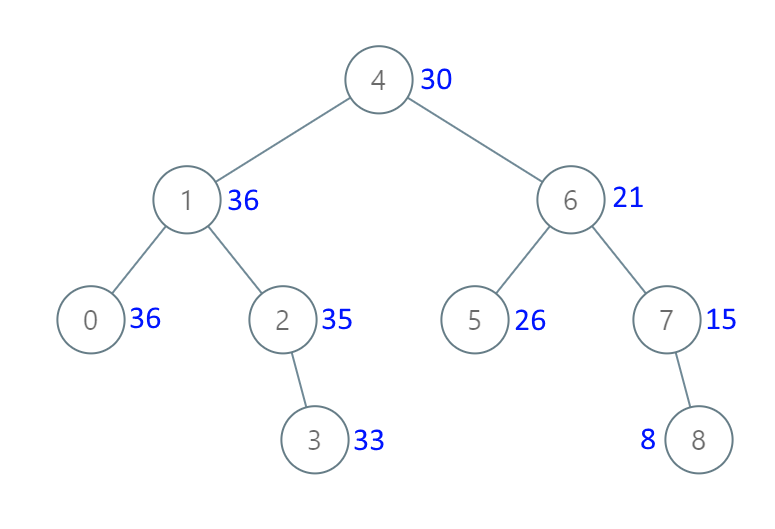
왼쪽과 오른쪽 값들이 각각 값의 크기에 따라 정렬되어 있는 트리를 의미

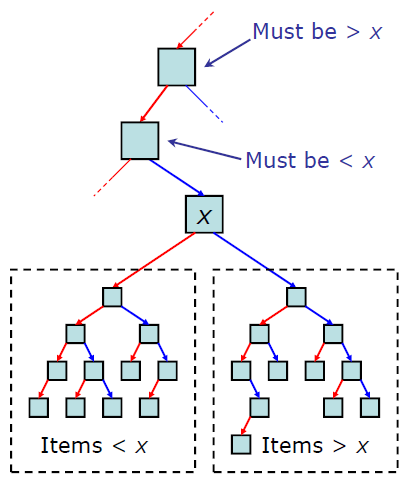
(이미지 출처 : https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/)

• 각 노드에 값이 있다.
• 중복된 노드가 없어야 한다.
• 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
• 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
• 좌우 하위 트리는 각각 다시 이진 탐색 트리여야 한다.
• 시간 복잡도가 O(log n)이다.

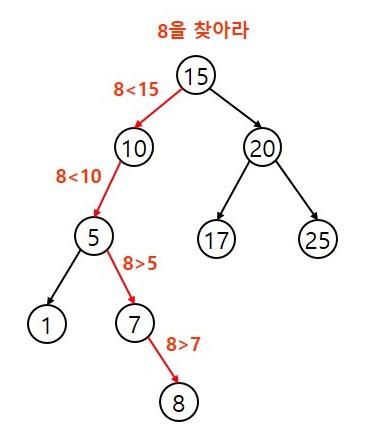
검색

• 검색하고자 하는 값 == X
• X를 루트 노드와 먼저 비교하고, 일치할 경우 루트 노드를 리턴
  • 불일치하고 X가 루트노드의 값보다 작을 경우 왼쪽 서브트리에서 재귀적으로 검색
  • 불일치하고 X가 루트노드의 값보다 큰 경우 오른쪽 서브트리에서 재귀적으로 검색

삽입

• 삽입하기 전, 검색을 수행
• 검색 후 일치하는 노드가 없으면 마지막 노드에서 키와 노드의 크기를 비교해 왼쪽이나 오른쪽에 새로운 노드 삽입

삭제

삭제하려는 노드의 자식 수에 따라

• 자식 노드가 없는 노드(리프 노드) 삭제 : 해당 노드를 단순히 삭제
• 자식 노드가 1개인 노드 삭제 : 해당 노드를 삭제하고 그 위치에 해당 노드의 자식노드를 대입
• 자식 노드가 2개인 노드 삭제 : 삭제하고자 하는 노드의 값을 해당 노드의 왼쪽 서브트리에서 가장 큰 값으로 변경하거나, 오른쪽 서브트리에서 가장 작은 값으로 변경한 뒤, 해당 노드(왼쪽 서브트리에서 가장 큰 값을 가지는 노드 or 오른쪽 서브트리에서 가장 작은 값을 가지는 노드)를 삭제

자가 균형 이진 탐색 트리

자가 균형(또는 높이 균형) 이진 탐색 트리는 삽입, 삭제 시 자동으로 높이를 작게 유지하는 노드 기반의 이진 탐색 트리

AVL 트리

각 노드에서 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이 차이가 1 이하인 이진 탐색 트리를 의미

• 균형 인수 : 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이
• 시간복잡도 O(log n)이다.

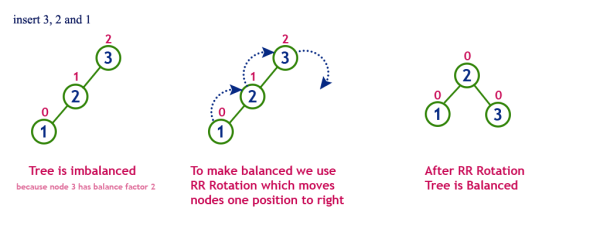
회전 동작

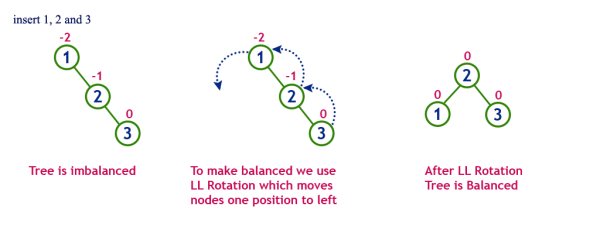
• LL 회전 : A로부터 N까지의 경로상의 노드들을 오른쪽으로 회전

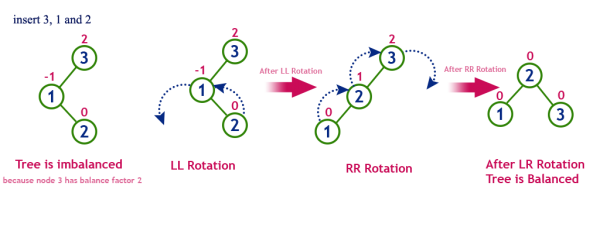
• LR 회전 : A로부터 N까지의 경로상의 노드들을 왼쪽-오른쪽으로 회전

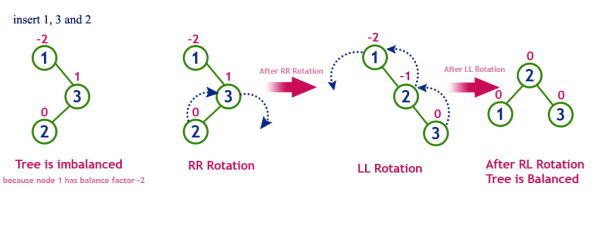
• RL 회전 : A로부터 N까지의 경로상의 노드들을 오른쪽-왼쪽으로 회전

• RR 회전 : A로부터 N까지의 경로상의 노드들을 왼쪽으로 회전

레드-블랙 트리

• 노드는 레드 혹은 블랙 중의 하나이다.
• 루트 노드는 블랙이다.
• 모든 리프 노드들(NIL)은 블랙이다.
• 레드 노드의 자식 노드 양쪽은 언제나 모두 블랙이다. (즉, 레드 노드는 연달아 나타날 수 없으며, 블랙 노드만이 레드 노드의 부모 노드가 될 수 있다.)
• 어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 리프 노드를 제외하면 모두 같은 개수의 블랙 노드가 있다.

위 조건들을 만족하면, 레드-블랙 트리는 루트 노드부터 가장 먼 경로까지의 거리가 가장 가까운 경로까지의 거리의 두 배 보다 항상 작다는 중요한 특성을 나타낸다.

트리 순회

트리 순회란 그래프 순회의 한 형태로 트리 자료구조에서 각 노드를 정확히 한 번 방문하는 과정을 말한다.

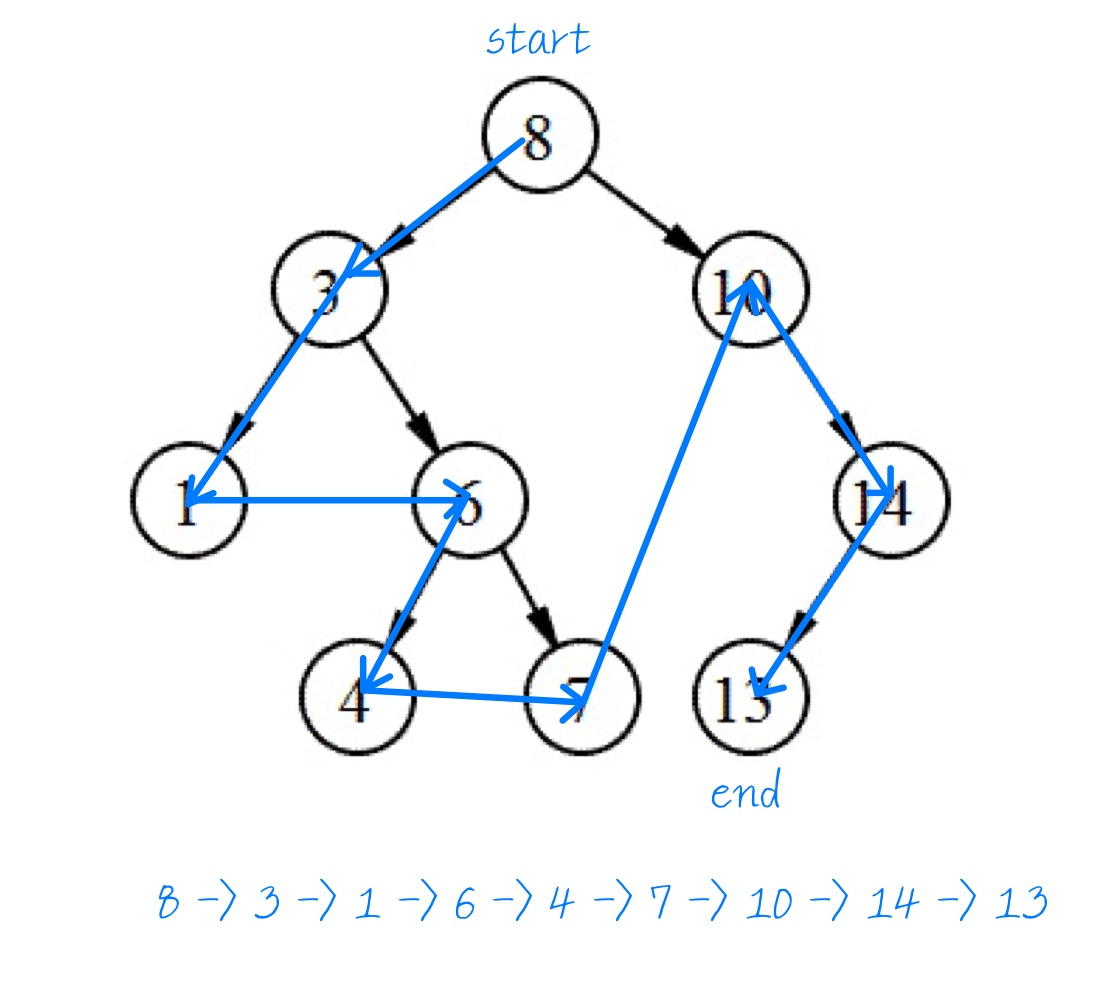
전위 순회(Preorder Traversal)

root -> left -> right

현재 노드 순회후 왼쪽과 오른ㅉ

코드

def preorder(node):
    if node is None:
        return
    print(node.val)
    preorder(node.left)
    preorder(node.right)

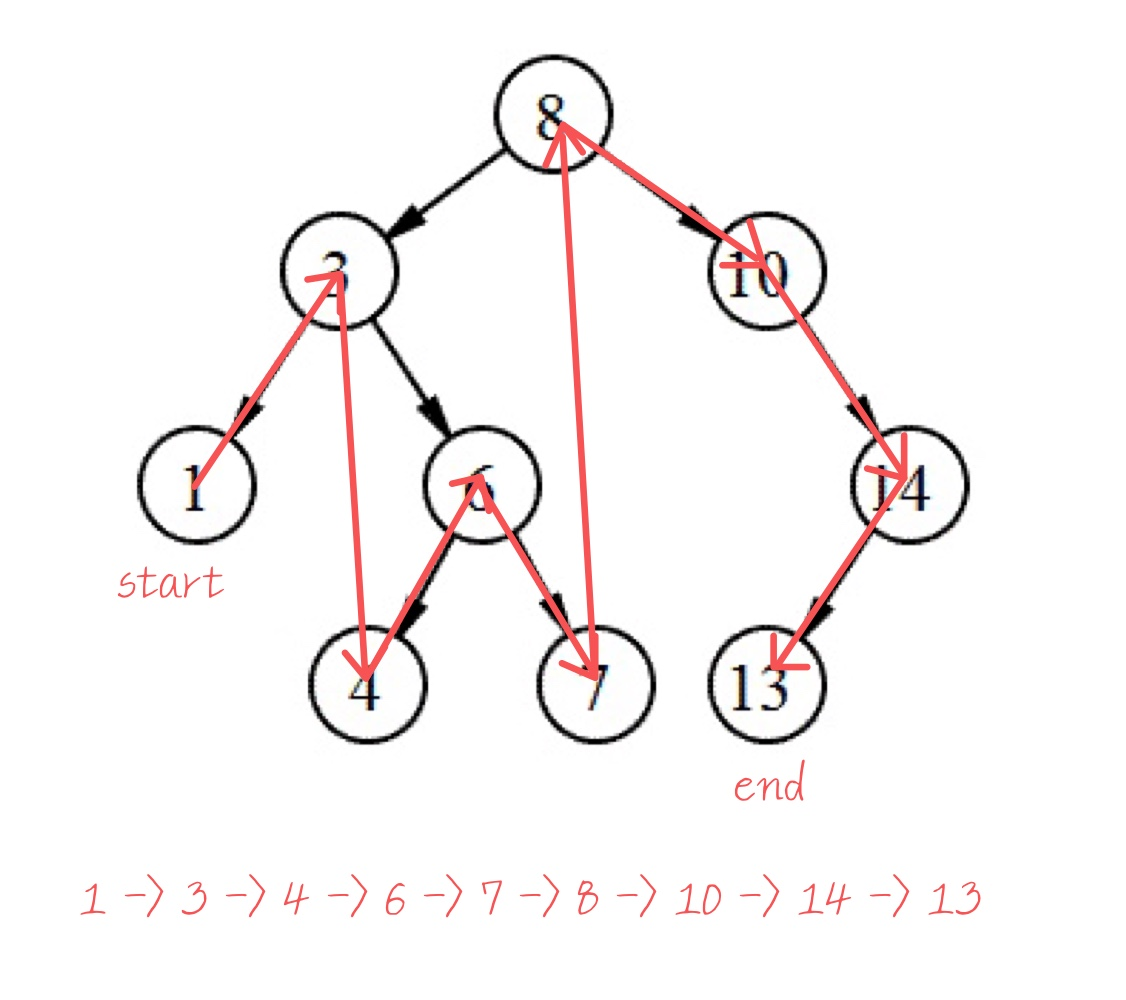
중위 순회(Inorder Traversal)

left -> root -> right

코드

def inorder(node):
    if node is None:
        return
    inorder(node.left)
    print(node.val)
    inorder(node.right)

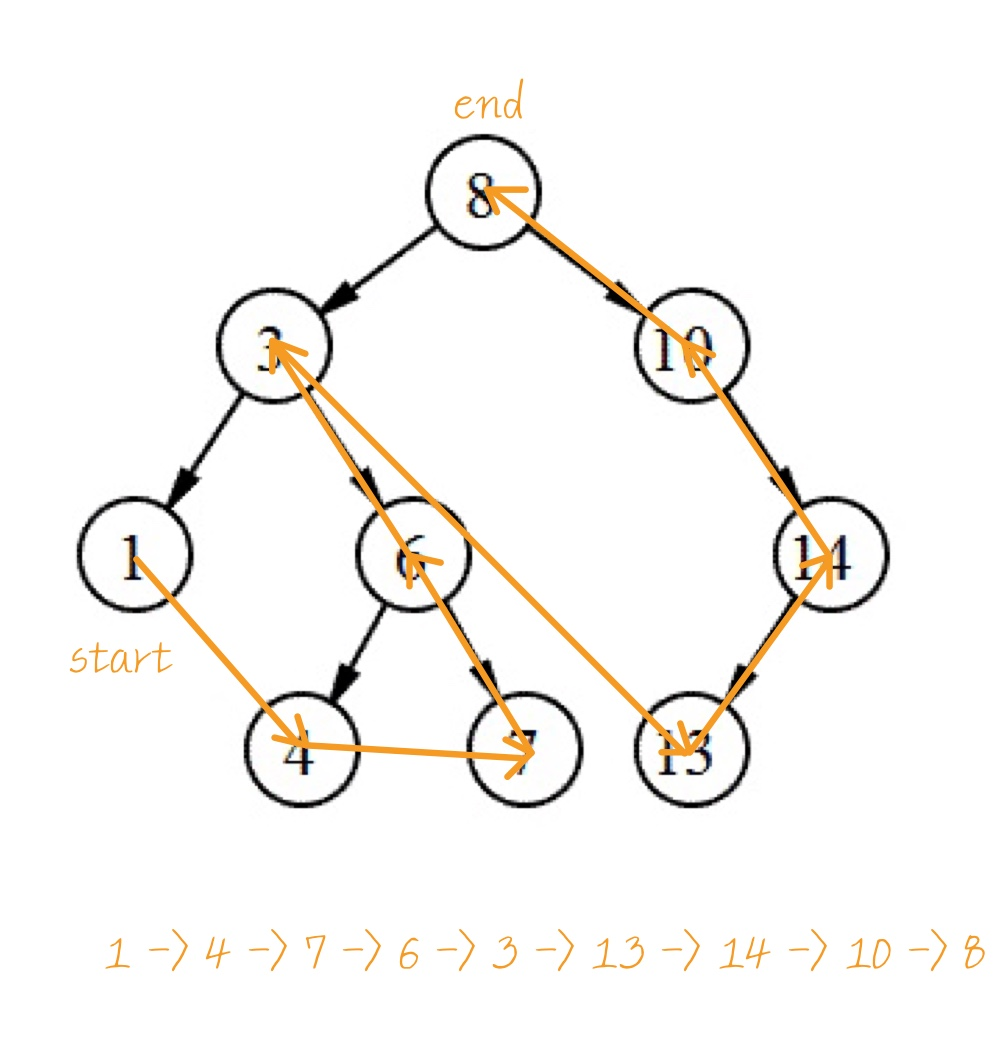
후위 순회(Postorder Traversal)

left -> right -> root

코드

def postorder(node):
    if node is None:
        return
    postorder(node.left)
    postorder(node.right)
    print(node.val)