파이썬 알고리즘 인터뷰_이진 트리

«파이썬 알고리즘 인터뷰 서적 내용을 정리»


문제01 정렬된 배열의 이진 탐색 트리 변환

https://leetcode.com/problems/convert-sorted-array-to-binary-search-tree

오름차순으로 정렬된 배열을 높이 균형 이진 탐색 트리로 변환하라.

Example:

Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
    / \
   -3   9
  /   /
 -10  5


  • 풀이1_이진 검색 결과로 트리 구성
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        if not nums:
            return None
        
        mid = len(nums) // 2
        
        # 분할 정복으로 이진 검색 결과 트리 구성
        node = TreeNode(nums[mid])
        node.left = self.sortedArrayToBST(nums[:mid])
        node.right = self.sortedArrayToBST(nums[mid + 1 :])
        
        return node

Result

Runtime : 76ms, Memory : 16.6MB


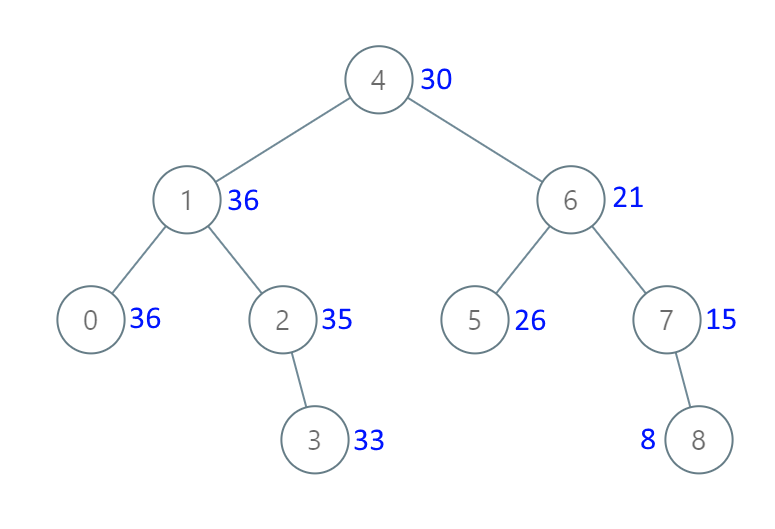
문제02 이진 탐색 트리(BST)를 더 큰 수 합계 트리로

https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree

BST의 각 노드를 현재값보다 더 큰 값을 가진 모든 노드의 합으로 만들어라.

Example 1:

img

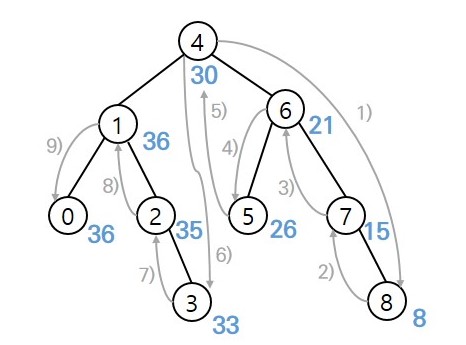
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2:

Input: root = [0,null,1]
Output: [1,null,1]

Example 3:

Input: root = [1,0,2]
Output: [3,3,2]

Example 4:

Input: root = [3,2,4,1]
Output: [7,9,4,10]


  • 풀이1_중위 순회로 노드 값 누적
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    val : int = 0
    def bstToGst(self, root: TreeNode) -> TreeNode:
        # 중위 순회 노드 값 누적
        if root:
            self.bstToGst(root.right)
            self.val += root.val
            root.val = self.val
            self.bstToGst(root.left)
            
        return root

Result

Runtime : 32ms, Memory : 14.3MB

bstt_sum


문제03 이진 탐색 트리(BST) 합의 범위

https://leetcode.com/problems/range-sum-of-bst

이진 탐색 트리(BST)가 주어졌을 때 L 이상 R 이하의 값을 지닌 노드의 합을 구하라.

Example 1:

img

Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32

Example 2:

img

Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23


  • 풀이1_재귀 구조 DFS로 브루트 포스 탐색
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        if not root:
            return 0
        
        return (root.val if  low <= root.val <= high else 0) + \
                self.rangeSumBST(root.left, low, high) +  \
                self.rangeSumBST(root.right, low, high)

Result

Runtime : 272ms, Memory : 22.3MB


  • 풀이2_DFS 가지치기로 필요한 노드 탐색
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        def dfs(node: TreeNode):
            if not node:
                return 0
            
            # 루트가 low보다 작은 경우, 왼쪽 서브 트리 가지치기
            if node.val < low:
                return dfs(node.right)
            # 루트가 high보다 큰 경우, 오른쪽 서브 트리 가지치기
            elif node.val > high:
                return dfs(node.left)
            # low <= root.val <= high인 경우
            return node.val + dfs(node.left) + dfs(node.right)
        
        return dfs(root)

Result

Runtime : 188ms, Memory : 22.3MB


  • 풀이3_반복 구조 DFS로 필요한 노드 탐색
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        stack, sum = [root], 0
        # 스택 이용 필요한 노드 DFS 반복
        while stack:
            node = stack.pop()
            if node:
                if node.val > low:
                    stack.append(node.left)
                if node.val < high:
                    stack.append(node.right)
                if low <= node.val <= high:
                    sum += node.val
        return sum

Result

Runtime : 192ms, Memory : 22.1MB


  • 풀이4_반복 구조 BFS로 필요한 노드 탐색
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        stack, sum = [root], 0
        # 스택 이용 필요한 노드 DFS 반복
        while stack:
            node = stack.pop(0)
            if node:
                if node.val > low:
                    stack.append(node.left)
                if node.val < high:
                    stack.append(node.right)
                if low <= node.val <= high:
                    sum += node.val
        return sum

Result

Runtime : 208ms, Memory : 22MB


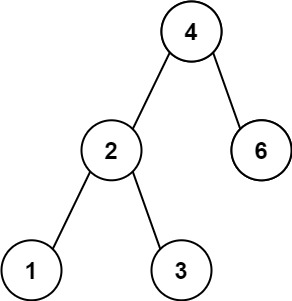
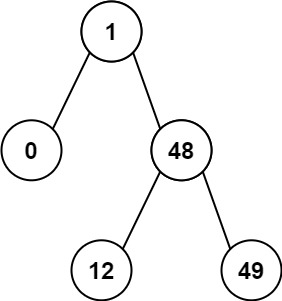
문제04 이진 탐색 트리(BST) 노드 간 최소 거리

https://leetcode.com/problems/minimum-distance-between-bst-nodes

두 노드 간 값의 차이가 가장 작은 노드의 값의 차이를 출력하라.

Example 1:

img

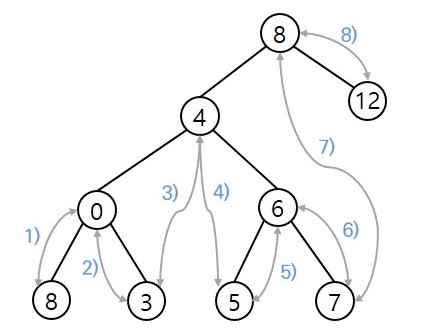
Input: root = [4,2,6,1,3]
Output: 1

Example 2:

img

Input: root = [1,0,48,null,null,12,49]
Output: 1
  • root와 가장 가까운 거리에 있는 노드는 왼쪽 서브 트리에서 가장 큰 값, 오른쪽 서브 트리에서 가장 작은 값이다.


  • 풀이1_재귀 구조로 중위 순회
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    prev = -sys.maxsize
    result = sys.maxsize
    
    # 재귀 구조 중위 순회 비교 결과
    def minDiffInBST(self, root: TreeNode) -> int:
        if root.left:
            self.minDiffInBST(root.left)
            
        self.result = min(self.result, root.val - self.prev)
        self.prev = root.val
        
        if root.right:
            self.minDiffInBST(root.right)
        
        return self.result

Result

Runtime : 28ms, Memory : 14.3MB

bst_shortest_distance


  • 풀이2_반복 구조로 중위 순회
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDiffInBST(self, root: TreeNode) -> int:
        prev = -sys.maxsize
        result = sys.maxsize
        
        stack = []
        node = root
        
        # 반복 구조 중위 순회 비교 결과
        while stack or node:
            while node:
                stack.append(node)
                node = node.left
                
            node = stack.pop()
            
            result = min(result, node.val - prev)
            prev = node.val
            
            node = node.right
            
        return result

Result

Runtime : 32ms, Memory : 14.2MB


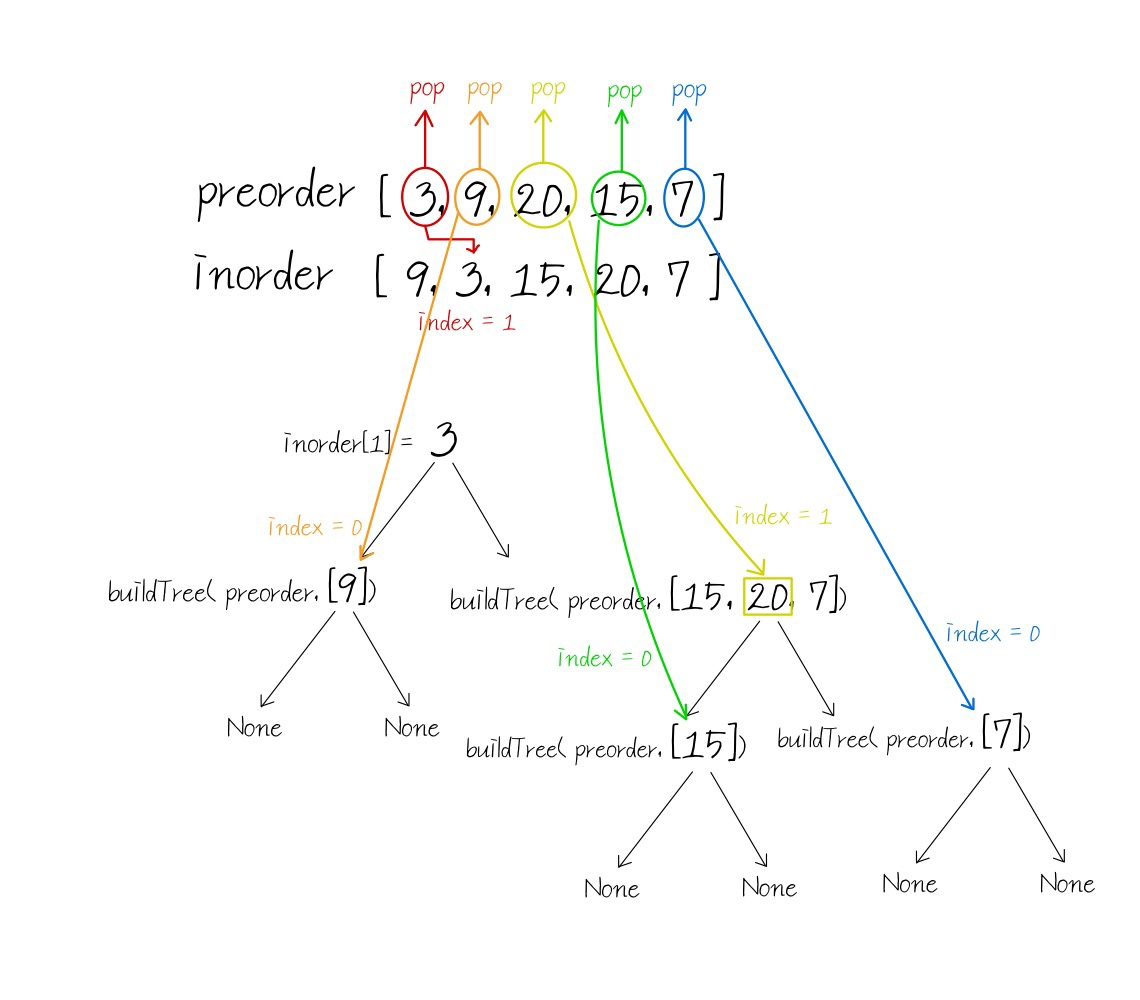
문제05 전위, 중위 순회 결과로 이진 트리 구축

https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal

트리의 전위, 중위 순회 결과를 입력값으로 받아 이진 트리를 구축하라.

Example

preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]

Return the following binary tree:

    3
   / \
  9  20
    /  \
   15   7


  • 풀이1_전위 순회 결과로 중위 순회 분할 정복
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if inorder:
            # 전위 순회 결과는 중위 순회 분할 인덱스
            index = inorder.index(preorder.pop(0))
            
            # 중위 순회 결과 분할 정복
            node = TreeNode(inorder[index])
            node.left = self.buildTree(preorder, inorder[0:index])
            node.right = self.buildTree(preorder, inorder[index + 1:])
            
            return node

Result

Runtime : 140ms, Memory : 53.2MB

image-20210219122143459